西暦から十二支を素早く求める

1. 左手の計算

1. 西暦の先頭1桁を見て、その値を3で割ったあまりを左手に作る。
2. 次の桁を見て、その値を3で割ったあまりを左手に足し込んでいく。ただし、足し込む際には以下のルール（3進数）に従う。つまり、結果は常に0、1、2のいずれかとなる。
• 1に2を足すと0になる。
• 2に1を足すと0になる。
• 2に2を足すと1になる。
3. すべての桁を処理するまで、2を繰り返す。

別法

• すべての桁を足し、その合計を3で割り、あまりを求める。その結果を左手に作る。
• ティップス1： 桁が3の倍数の場合、足す必要はない。
• ティップス2： 集計の中間結果や総計が10以上（つまり2桁）になった場合、それら各桁を足してもよい。

2. 右手の計算

1. 西暦の下2桁だけを使用する。まず、右手で「グー」を作る。
2. 西暦の下2桁が奇数であれば、親指を立て、下2桁に1を足す。
• その値を2で割る。
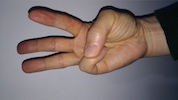
• 奇数であれば、指2本（人差し指と中指）を開く（親指は握りこんで構わない[*1]）。
• 偶数であれば、何もしない（親指は握りこんで構わない[*1]）。
3. 西暦の下2桁が偶数であれば、人差し指を開く。
• 下2桁を2で割る。
• 奇数であれば、指2本（中指と薬指）を開く。
• 偶数であれば、何もしない。

[*1] ちなみに奇数の際に親指を立てるのは、下2桁に1を加算することを忘れないようにするための「きっかけ」に過ぎず、親指は結果の手のかたちとはまったく関係ない。

図解--右手の遷移図

下2桁は奇数か偶数か？	→→→→→ 奇数	下2桁に1を足し、 2で割った値は奇数か偶数か？	→→→→→ 奇数	指を2本足す
↓		↓偶数 何もしない
↓偶数
↓
2で割った値は奇数か偶数か？	→→→→→ 奇数	指を2本足す
↓偶数 何もしない

3. 結果の見方（形で憶えると西暦から数秒で十二支を求められるようになる）

子	丑	寅	卯
辰	巳	午	未
申	酉	戌	亥

ちょっとした考察

　子は両手がそれぞれ1と1、以降は丑、寅、卯・・・と順番に左手は「0, 1, 2, 0, 1, 2, ･･･」の繰り返し、右手は「0, 1, 2, 3, 0, 1, 2, 3, ･･･」の繰り返しとなる。

　式で書くと、（（（左手＋3）−右手） mod 3）×4＋右手　となる（答えは1が子、2が丑、3が寅、・・・0が亥となる／なお mod は剰余を求める演算子）。